2ο Εργαστήριο

Προδιαγραφές.
- Προδιαγραφή του $v_{a}$
Συνάρτηση μεταφοράς κλειστού βρόχου
Σφάλμα Θέσης
Μελέτη με $k = 1.5$
Closed Loop TF για το $T$
Ανάλυση των ΣΜΚΒ
Στροφές κινητήρα
Υπολογισμός DC Gains
Σύγκριση με την μελέτη ανοιχτού βρόχου:
Στροφές σε steady state
Ανάλυση σε matlab
Σύγκριση προδιαγραφών OL, CL
Απόκριση στροφών σε κλιμακωτού τύπου φορτίο
Bode HV
Bode HT

Σύστημα κλειστού βρόχου ίδιου τύπου με την προηγούμενη φορά μόνο που έχει προστεθεί μοναδιαία αρνητική ανάδραση

\begin{matrix} (1) & H T (s) = \frac{2.92 (s + 440)}{s + 12.064} \end{matrix}

\begin{matrix} (2) & H V (s) = \frac{18.69}{s + 12.064} \end{matrix}

Προδιαγραφές.

Ώστε να προσδιορίσουμε κατάλληλα τον ελεγκτή k

Μηδενική υπερύψψση για τις στροφές $ω (t), Ω (s)$

2 Σφάλμα μόνιμης κατάστασης θέσης μηδενικό για το ΣΚΒ:.

\begin{matrix} (3) & e_{s s} = 0, ω_{δ, s s} = V \end{matrix}

Χρόνος ανόδου $t_{a} \leq 160 m s$
Τάση διέγερσης $v_{a} (t) \leq 350 V$
$V = 150 V$
$ω_{δ, m a x} = 200 r a d / s e c$

Προδιαγραφή του $v_{a}$

Πρέπει ανεξαρτήτως εισόδου $v_{a} \leq 350 V$

\begin{matrix} (4) & v_{a} = (v - ω) * k = e_{m a x} * k \Rightarrow \dots k \leq 1.75 \end{matrix}

Συνάρτηση μεταφοράς κλειστού βρόχου

Από την αρχή της επαλληλίας, παίρνοντας $T_L = 0$$

\begin{matrix} (5) & \HV_{k} (s) = \frac{18.69 k}{s + (12.064 + 18.69 k)} \end{matrix}

Οπότε παρατηρούμε πως ο πόλος του closed loop μετακινείται προς τα αριστερα. Δεν μένει δηλαδή στο -12. Είναι καλό αυτό (γιατί?). Βέβαια δεν μπορεί να πάει πολύ πιο αριστερά λόγω των προδιαγραφών.

Σφάλμα Θέσης

Από την θεωρία γνωρίζουμε πως:

\begin{matrix} (6) & \e_{s s p} = \frac{1}{1 + k_{p}} = \frac{12.064}{12.064 + 128.69 k} \neq 0 \end{matrix}

Επομένως, όσο αυξάνει το κέρδος μειώνεται το σφάλμα στην μόνιμη κατάσταση.

Μελέτη με $k = 1.5$

Γιατί όμως πήραμε 1.5 και όχι 1.75?

k = 1.5;
nHVK = [18.69*k];
dHVK = [1 12.064+18.69*k];

HVk = tf(nHVK,dHVK)

Closed Loop TF για το $T$

Οι πράξεις εδώ δεν έγιναν θεωρήθηκε δεδομένο

nHTK = -1*[2.92 2.92*440];
dHTK = [1 40.1];

HTk = tf(nHTK,dHTK)

Ανάλυση των ΣΜΚΒ

Ο πόλος μας πήγε στο -40, ενώ έχουμε ακόμα ένα μηδενικό…

Στροφές κινητήρα

Απολύτως αναμενόμενα βάση της θεωρίας:

\begin{matrix} (7) & Ω (s) = H V_{k} (s) V (s) + H T_{k} (s) T_{L} (s) \end{matrix}

Υπολογισμός DC Gains

Θυμίσου από θεωρία dcgain = Tf(0)

HVk0 = dcgain(HVk)
HTk0 = dcgain(HTk)
essp = 12.064/( 12.064+18.69*k )

Σύγκριση με την μελέτη ανοιχτού βρόχου:

Παρατηρούμε πως τα dcgain έχουν και στις0δύο περιπτώσεις μεωθεί, οδηγώντας σε μια μεγαλύτερη μείωση του σφάλματος με είσοδο μοναδιαία βηματική συνάρτηση.

Στροφές σε steady state

Από FVT:

\begin{matrix} (8) & ω_{δ, s s} = lim_{s \to 0} s * Ω (s) = \dots \end{matrix}

Στην διαφάνεια 6 φανερώνεται η σύγκριση για ανοιχτό και κλειστό βρόχο.

Ανάλυση σε matlab

figure(3)
step(150*HV)
hold on
step(150*HVk)

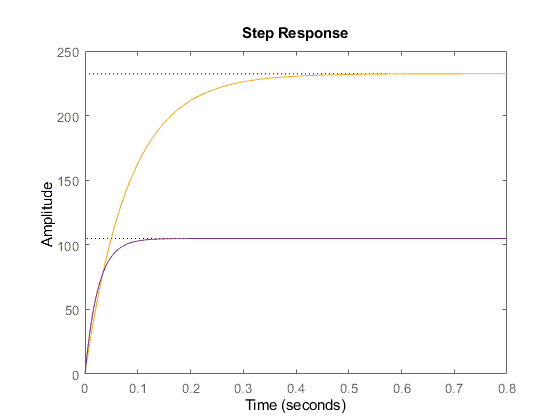
Σύγκριση προδιαγραφών OL, CL

Rise time -> πτώση από τα 180+ στα 54, υπερκαλύπτοντας τις προδιαγραφες
Settle Time -> από 324+ στα 97

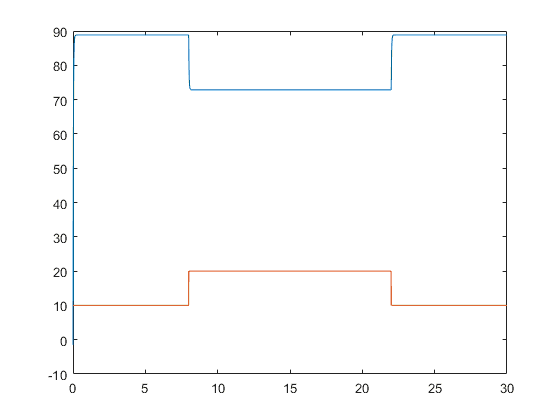
Απόκριση στροφών σε κλιμακωτού τύπου φορτίο

Το γράφω μόνο για ορολογία Δειγματοληψία του χρόνου απο 0 εως 30 με 10ms sampling time

figure(4);
t = 0 : 0.01 : 30;
uV = 150 * stepfun(t,0);
yV = lsim(HVk, uV, t);

uT = 0.5 * stepfun(t,0) + 0.5 * stepfun(t, 8) + -0.5 * stepfun(t, 22);
yT = lsim(HTk, uT, t);

y = yV + yT;
plot(t, y, t, 20*uT)

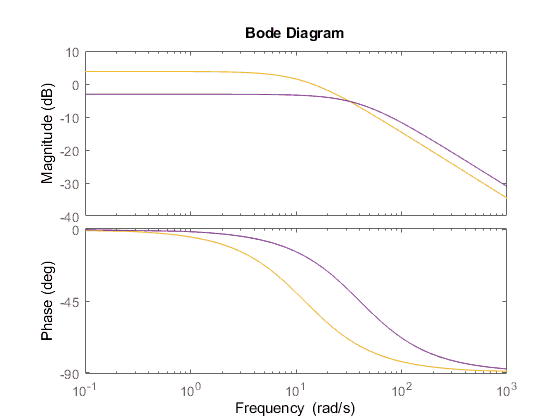
Bode HV

figure(5)
bode(HV)
hold on;
bode(HVk)

Bode HT

figure(6)
bode(HT)
hold on;
bode(HTk)

2ο Εργαστήριο

Table of Contents